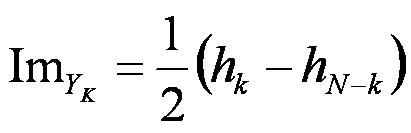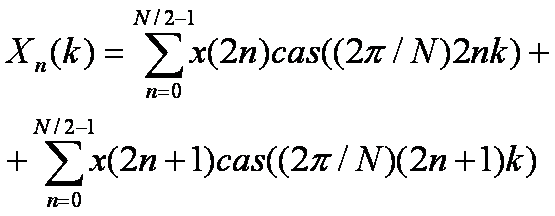Часть 2. Как научить безмозглый процессор спектральным преобразованиям.
Итак, у нас есть реальность, данная нам в ощущениях. То есть процессор ATMega32A в лучшем случае, и ATMega16 (или 8) – в худшем, у которого всё что есть – это 8-битное АЛУ с сумматором да умножателем. А нам хочется обработать спектр сигнала Доплера… хотя бы.
Не буду тянуть кота за хвост в долгий ящик: ДПФ отпадает как класс. Во-первых, комплексная арифметика; во-вторых… да ему памяти не наямисси с его комплексными массивами и отрицательными частотами в двух местах. Да, есть варианты ДПФ, в которых вычисляется только действительная область, но… посмотрев чужие исходники, пришел к выводу что это тоже достаточно длинно и нудно.
Что ж… есть альтернатива для ДПФ – это дискретное преобразование Хартли (ДПХ). Оно не очень известно, дело в том, что срок патента на его использование истек лишь недавно, и только после этого оно стало более-менее доступно.
ДПХ действительного вектора а – это действительный вектор с координатами
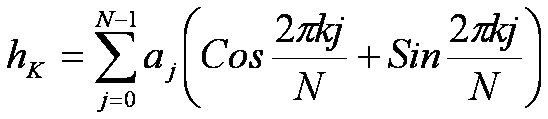
И никаких комплексных чисел. Казалось бы, что может дать преобразование по функции, являющейся лишь сдвинутым по фазе синусом:

Да много чего.
В частности, обратное преобразование Хартли отличается от прямого лишь наличием множителя 1/N
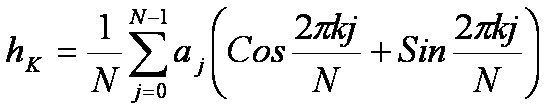
То есть одну и ту же функцию можно использовать как для прямого, так и для обратного преобразования.
Для ценителей Фурье-преобразования будет приятно узнать, что между Фурье и Хартли существует однозначная связь:
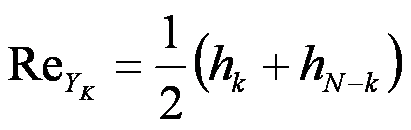
Начинаем вычислять БПХ так же, как и Фурье. Для начала ДПХ разделяет массив x(n) длиной N на два массива длиной N/2 – x1(n) и x2(n). Два массива преобразуются в Xh1(k) и Xh2(k) и комбинируются в один массив Xh(k), но в отличие от Фурье – в соответствии с выражением
Подобно ДПФ, второе слагаемое в уравнении (4) не является ДПХ, поскольку временная последовательность x2(n) сдвинута влево. Последовательность x2(n) должна быть сдвинута влево на 1 по правилам сдвига ДПХ, т.е. по формуле
Где С – некоторая константа. После сдвига x2(n) по выражению (5), выражение (4) принимает вид
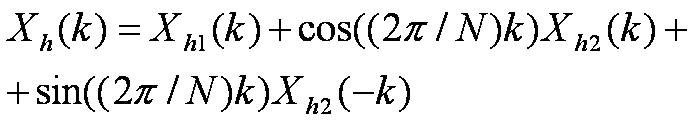
Где Xh1(k) – это преобразование Хартли от x1(n), а Xh2(k) – соответственно, от x2(n). Использованием правила сдвига два N/2-точечных преобразования Хартли могут быть объединены в одно.
Правила вычисления значений Xh(k) при k≤N/2 те же самые, что и в Фурье-преобразовании. Использование периодических свойств позволяет вычислять значения Xh(k) для всего диапазона N следующим выражением:
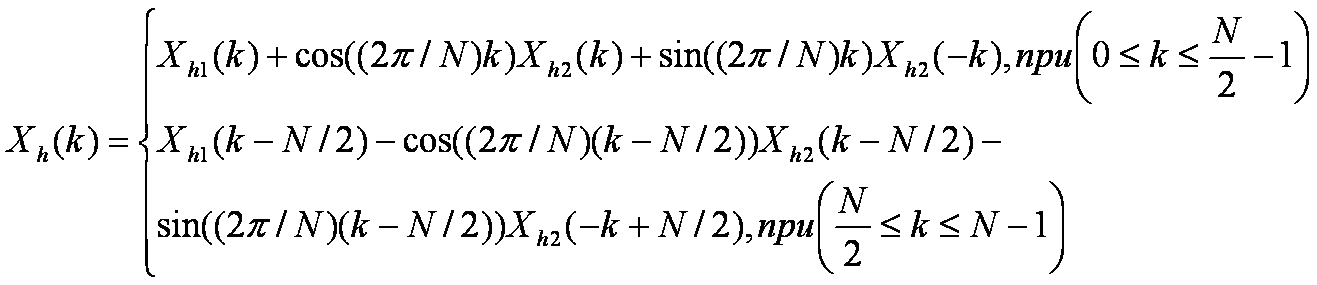 (6)
(6)
Это выражение и является базовым для построения преобразования ДПХ.
Основная разница с ДПФ является то, что из трех значений получается два, т.е. требуется «двойная бабочка» для вычислений. На рисунке показана двойная бабочка вычисления 8-точечного преобразования как двух 4-точечных.
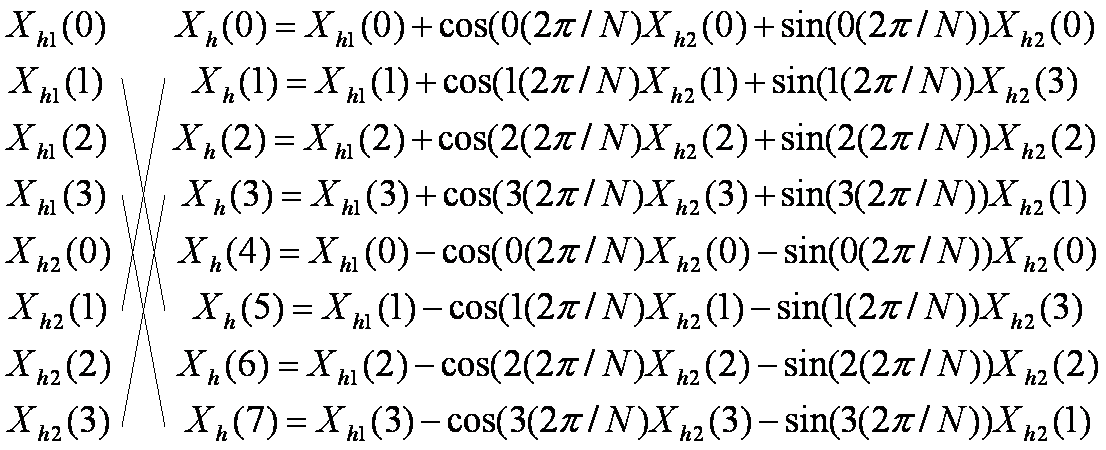
Двойная бабочка использует 4 входа и генерирует 4 выхода. Есть причины, почему выражение (6) при этом генерирует лишь три выхода. В соответствии с (6), выход Xh(1) требует входов Xh1(1), Xh1(3), Xh2(1), Xh2(3). Поскольку Xh2(k) неопределен для k<0, потребовалось вхождение, идентичное отрицательным частотам. Для этого отрицательные частотные компоненты для N- точечной последовательности сохраняются после N/2-й точки. В общем виде формула для вычисления положения отрицательной частоты:
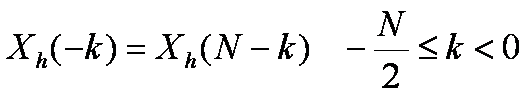
Например, для Xh2(-1)
![]()
Выходы Xh(0), Xh(2), Xh(4), Xh(6) – требуют только двух входов. Причина этого заключается в том, что для них нет соответствующих им отрицательных частот. В действительности, Xh(2) и Xh(-2) являются частотами Найквиста для 4-точечной последовательности, и Xh(2) = Xh(-2).
Уф. Полагаю, теперь можно привести реализацию этого темного алгоритма, написанную на Pascal.
procedure RFHT(var fx:array of real; m: integer);
Var
arg,temp1,temp2,fcos,fsin,dsin,dcos,scale:real;
k,butdis,butloc,n,istep,len,Times: Integer;
Begin
//
len:=1 shl m;
rbitrev(fx,m);
arg:=3.14159265358979323;
n:=1;
Times:=0;
nb := 0;
repeat
istep:=2*n;
dcos:=cos(arg);
dsin:=sin(arg);
arg:=arg/2;
fcos:=dcos;
fsin:=dsin;
k:=0;
while k<(len) do
begin
// Цикл считает нулевую частоту
temp1:=fx[k+n];
fx[k+n]:=fx[k]-temp1;
fx[k]:=fx[k]+temp1;
k:=k+istep;
end;
if n>2 then
begin
butdis:=n-2;
for butloc:=2 to (n div 2) do
begin
k:=butloc-1;
while k<(len) do
begin
// двойная бабочка
temp1:=fcos*fx[k+n]+fsin*fx[k+n+butdis];
temp2:=fsin*fx[k+n]-fcos*fx[k+n+butdis];
fx[k+n]:=fx[k]-temp1;
fx[k+n+butdis]:=fx[k+butdis]-temp2;
fx[k]:=fx[k]+temp1;
fx[k+butdis]:=fx[k+butdis]+temp2;
//
k:=k+istep;
end;
temp1:=fcos*dcos-fsin*dsin;
fsin:=fsin*dcos+fcos*dsin;
fcos:=temp1;
butdis:=butdis-2;
end;
end;
if n>1 then
Begin
k:=(n div 2);
while k<(len) do
Begin
// цикл частот Найквиста
temp1:=fx[k+n];
fx[k+n]:=fx[k]-temp1;
fx[k]:=fx[k]+temp1;
k:=k+istep;
End;
end;
n:=istep;
until n>=len;
End;
Ну а функция бит-реверсной перестановки – достаточно тривиальна, их немало бродит в Интернете:
procedure TForm1.rbitrev(var x: array of real; m: integer);
var
itab: array [0..257] of integer;
m2,nbit,imax,lbss,i,j,k,l,j0: integer;
t1: real;
begin
for i := 0 to 257 do itab[i] := -1;
m2:=m div 2;
nbit:=1 shl m2;
if 2*m2<>m then m2:=m2+1;
itab[1]:=0;
itab[2]:=1;
imax:=1;
for lbss:=2 to m2 do
begin
imax:=2*imax;
for i:=1 to imax do
begin
itab[i] :=2*itab[i];
itab[i+imax]:=1+itab[i];
end;
end;
for k:=2 to nbit do
begin
j0:=nbit*itab[k];
i:=k-1;
j:=j0;
for l:=2 to itab[k]+1 do
begin
t1:=x[i];
x[i]:=x[j];
x[j]:=t1;
i:=i+nbit;
j:=j0+itab[l];
end;
end;
end;
Это, что называется, «лобовая» реализация. Она избыточна в плане вычисления коэффициентов доворота векторов на каждом шаге преобразования. Как можем заметить, вычисление их начинается с π, зтем аргумент делится на 2, а промежуточные значения вычисляются по формулам
![]()
![]()
Используя периодические свойства функций можно построить достаточно короткую таблицу; кроме того, если построить ее для cos(x) – значения sin(x) можно получить, просто читая ее с другого конца. Таким образом, получается, что таблица нам нужна всего лишь длиной N/4-1 элементов. Не мудрствуя лукаво, посчитаем ее заранее следующей функцией (Pascal), и введем в программу как переменную компиляции. Ну, или просто будем считать ее заранее и складывать где-нибудь в уголочке – всё зависит от имеющихся в нашем распоряжении вычислительных ресурсов.
procedure TMainCTLForm.Button2Click(Sender: TObject);
Var
M2: Integer;
i: Integer;
arg, darg: Double;
cos_val: Double;
// Пример расчета коэффициентов доворота для С-шной реализации
// преобразования Хартли
begin
Memo1.Clear;
M2 := StrToInt(LabeledEdit1.Text);
arg := Pi/(1 shl (M2-1));
darg := arg;
for i := 0 To (1 shl (M2-2))-2 Do
Begin
cos_val := Cos(arg);
arg := arg + darg;
Memo1.Lines.Add(Format(' %.9f * 32768,//[%d]',[cos_val, i]));
End;
end;
И точно так же сформируем таблицу для битреверсной перестановки
procedure TForm1.Button2Click(Sender: TObject);
Var
itab: array [0..257] of integer;
M, m2,nbit,imax,lbss,i: integer;
begin
M := StrToInt(Edit1.Text); // длина как степень 2-х
for i := 0 to 257 do itab[i] := -1;
m2 := M div 2;
if (2 * m2) <> m then m2 := m2 + 1;
itab[1] := 0;
itab[2] := 1;
imax := 1;
for lbss := 2 to m2 do
begin
imax := 2 * imax;
for i:=1 to imax do
begin
itab[i] :=2 * itab[i];
itab[i+imax]:=1 + itab[i];
end;
end;
//
imax := (1 shl (M2))+1;
Memo1.Lines.Clear;
memo1.lines.Add('//массив перестановок');
memo1.lines.Add('unsigned char __flash itab['+IntToStr(imax)+']={');
memo1.Lines.Add(' 255,// [0]');
for i:=1 to imax-1 do
memo1.Lines.Add(Format(' %2d, // [%d]',[itab[i],i]));
memo1.lines.Add('};');
end;
Реализация утилиты, считающей коэффициенты и перестановки - в приложении. С-шный текст программы, полученный с помощью этой утилиты – в приложении. описание программы – в следующей части. Реализация – целочисленная, с фиксированной точкой формата 1.15 (знаковый бит, и 15 бит после запятой). Поэтому и размерность преобразования получается небольшая – 256 точек максимум, при размерности массива 16 бит и входных данных – 8 бит. Тогда удается избежать переполнения при суммировании.